Odkud to Slunce svítí

Světlo ze Slunce letí k nám na Zemi asi 500 s. Lidé vědí, že proto vidíme Slunce vlastně o 500 s mladší, než právě je, a mají pravdu. Často se ale domnívají, že také Slunce vidíme vlastně jinde, než je, a to o cca 2° pozadu na jeho cestě. Když se za 24 h = 24 × 3600 s otočí kolem Země o 360°, tak za 500 s, než k nám světlo od něj doletí, uběhne Slunce úhel 360°×500 / ( 24×3600) ≈ 2,08°.Tato úvaha je však chybná. Diskutovali jsme o ní v článku http://www.3pol.cz/cz/rubriky/bez-zarazeni/1682-kde-je-slunce-na-obloze, ale diskutující si přáli ještě dalšího vysvětlení.

Slunce je totiž přesně v tom směru, odkud ho vidíme! (Zanedbáváme jen aberaci (A) danou ročním pohybem Země kolem Sluncea refrakci (B) v atmosféře, obojí je vysvětlené na konci článku.)

Heliocentrická soustava

Z heliocentrického (Koperníkova) pohledu je situace jasná. Žádný zdánlivý pohyb Slunce po obloze se nekoná, Slunce stojí v prostoru pevně, ale Země se otáčí kolem své osy a vytváří si tím den a noc. (Roční oběh Země kolem Slunce po kružnici má jen nepatrný vliv (viz vysvětlení (A)). Foton letí od Slunce po přímce k Zemi, někam na ni dopadne a směr, odkud dopadl, ukazuje na Slunce, ať se Země točí, jak je jí libo. Kdyby ji zlý obr zastavil a roztočil jinak, dopadl by foton na Zemi ovšem jinam, ale zase ze směru, odkud byl Sluncem vyslán. Žádný problém.

Geocentrická soustava

Správný popis z geocentrického (Ptolemaiova) pohledu je složitější, protože je to neinerciální systém. Země v něm stojí, ale Slunce i všechny hvězdy se kolem ní točí v kruzích a fotony letící od nich rovnou k Zemi se tedy vzhledem k Zemi kolem ní ovíjejí po spirálách majících tolik závitů, kolik dnů a nocí jsou fotony na cestě. Od Slunce je to sice jen oblouček – viz obrázek – ale i tak nikoli přímka! Proto tečna k tomuto obloučku v místě dopadu na Zemi neukazuje na S‘, kde Slunce před 500 s bylo (tam vede oblouček), ale na S, kde právě teď Slunce je!

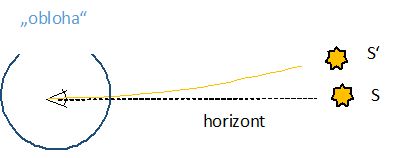
Pozorováno z boku, letí od Slunce S‘ na Zem světelný paprsek nikoli po přímce, ale po svislém oblouku s  vodorovnou tečnou v místě dopadu. S je poloha Slunce, když my vidíme západ, S‘ poloha Slunce 500 sekund před tím, tj. když paprsek vyslalo. Astronomickou refrakci (B) ani aberaci (A) zde neuvažujeme.

Dokonce i budovat mechaniku v takové (neinerciální) soustavě jde; musíme však doplnit tzv. „setrvačné síly“, tj. unášivou, odstředivou, Coriolisovu, apod. Ty pak donutí naše Slunce řítit se kolem Země šílenou rychlostí, větší než třetina světelné rychlosti, aby za den a noc oběhlo kružnici o poloměru 150 milionů kilometrů. U hvězd podstatně vzdálenějších si tu rychlost (opět vůči neotáčející se Zemi!) ani nepřejte znát. Díky těmto silám pak letí – ze Země popisováno – světelný paprsek po výše zmíněném oblouku. Ukážeme si to na mírnějším a názornějším příkladu s kolotočem.

Příklad s kolotočem

Kolega K sedí na kolotoči, já (J) na něho z chodníku házím míčem. Mému popisu z hlediska chodníku (já jsem nehybný) odpovídá heliocentrický popis Koperníkův, popisu ze soustavy kolotoče (K je nehybný) odpovídá geocentrický systém Ptolemaiův.

Popis z chodníku (Koperník): Já stojím, mířím před otáčejícího se kolegu tak, aby mi vjel právě do rány. Shora pozorováno,letí míč vůči chodníku po přímce (nevšímáme si pádu v tíhovém poli) a udeří kolegu přesně ze směru, odkud házím já.

Popis z kolotoče (Ptolemaios): Já se točím (spolu s celou okolní krajinou) kolem osy kolotoče, na němž sedí nehybný kolega K, míč letí vůči kolotoči po spirále, ale když na kolegu K dopadne, jsem já opravdu ve směru, odkud míč přiletěl.

Přiložené obrázky i animace to jistě přiblíží. (Animaci si můžete stáhnout do počítače ve formátu PPS, ve statické podobě ji najdete v galerii.)

Klíčový myšlenkový pokus: zrušme den a noc!

Podle Ptolemaia: zastavme Slunce na jeho dráze kolem Země; podle Koperníka: zastavme okamžitě otáčení Země. Zastaví se pro nás Slunce na obloze ihned (Koperník), anebo až za 500 s ≈ 8 minut (Ptolemaios v chybné verzi), až k nám světlo ze (zastaveného) Slunce doletí? Zastaví se zřejmě ihned! Samozřejmě, pokud „zhasneme Slunce“, poznáme to v obou popisech až za 8 minut. Ale „zhasnutí Slunce“ se taky odehrává v prostoru jinde (S), než zastavení rotace Země (Z).

Komu přijde zatěžko zastavit otáčející se Zemi, ať si představí pokus: já s otáčející se plošinkou a kolega K dojdeme na severní pól. On bude stát na zemi (a tedy otáčet se vůči Slunci, resp. Slunce se bude točit z hlediska Země kolem něj), já stojím na plošince zvolna se otáčející vůči Zemi jednou za den a noc proti hodinovým ručičkám (já se tedy vůči Slunci neotáčím a celou dobu mi Slunce svítí přímo na obličej z jediného místa na obloze). Kde by mělo být Slunce v okamžiku, kdy K bude otočen jako já?, No samozřejmě pořád tamtéž, proti mně. A tedy i tam, kam se v tomto okamžiku právě K dívá. O žádné 2°pozadu! (Já jsem zde ve funkci oné obrem zastavené Země.)

A jak vypadá fyzika z hlediska kolotoče? Proč se já točím po kružnici? Označme mou vzdálenost od osy kolotoče r a úhlovou rychlost kolotoče vůči chodníku ω. Abych se já s hmotností m točil vůči kolotoči opačnou rychlostí (–ω) ve vzdálenosti r od osy, musí na mne působit výsledná síla

F = –mv²/r.

směřující ke středu otáčení. Ta vznikne součtem setrvačných sil, a to odstředivé (mv²/r, bohužel opačného směru, než potřebujeme pro výsledek) a Coriolisovy: –2mvω (na štěstí směrem ke středu). Protože je však v = ωr, dává jejich součet právě správnou velikost pro správný pohyb po kružnici správnou rychlostí. Je to trochu složitější, ale to je daň, kterou platí kolega K za to, že počítá v neinerciálním systému (v němž stojí na místě a netočí se).

Dodatky pro puntičkáře

(A) – aberace:

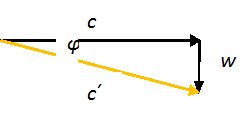
Postupná rychlost daná denním otáčením Země je jen cca 400 m/s, ale postupná rychlost daná ročním oběhem Země už činí 30 km/s, a tomu odpovídající úhel φ ≈ 22,4“ je malý, ale už změřitelný.Je-li složka w rychlosti pozorovatele kolmo k fotonu srovnatelná s rychlostí c světla, je nutno naklonit tubus dalekohledu (směr pohledu) tak, aby okulár zatím „neujel“, tedy o úhel φ takový, že tg φ = w/c.

(B) – astronomická refrakce:

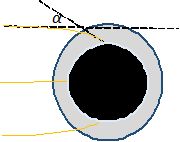
Paprsek (dráha fotonu) vcházející prakticky z vakua do stále hustších vrstev atmosféry se láme ke kolmici. Největší odchylka (α ≈ 0,5°) je tedy při letu tečném k Zemi (východ a západ Slunce), naopak při kolmém dopadu v poledne by byla nulová.

Obě směrové odchylky (A) i (B) jsou zřejmě výrazně menší, než (chybně) očekávaná odchylka 2°.

(Autor děkuje za podnětnou diskusi Josefu Dobranskému a Jakubovi Vošmerovi.)